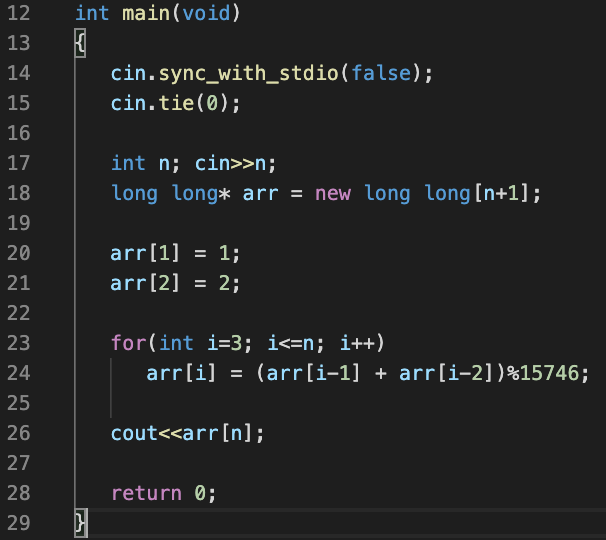
dp는 점화식 문제에도 자주 응용되지만 경우의 수와도 큰 연관이 있다. 그리고 놀랍게도 이 문제는 점화식 문제이면서도 경우의 수와도 연관이 있다. n이 4인 경우를 생각해보자. xxxx는 00xx 또는 1xxx 두 경우로 나누어진다. 이렇게 작은 식으로 쪼개지다 보면 n이 1인 경우와 2인 경우로 나뉘어진다. 따라서 가장 작은 단위를 정의해놓고 반복문으로 처리해준다.
코드를 써놓고 보니 피보나치 수열이라는 것을 알 수 있었다. 경우의 수에 대한 표현이 점화식으로 연결되었다.
'PS' 카테고리의 다른 글
| 백준 1932번: 정수 삼각형 C++ Code (0) | 2020.09.16 |
|---|---|
| 백준 1149번: RGB거리 C++ Code (0) | 2020.09.13 |
| 백준 1003번: 피보나치 함수 C++ Code (0) | 2020.09.13 |
| 백준 2748번: 피보나치 수 2 C++ Code (0) | 2020.09.13 |
| 에라토스테네스의 체 (0) | 2020.08.17 |



